|
Two Angles and an Included Side
Example
A triangle has 2 angles of 75° and 25° and the included side is 5. What is the other angle and
the other 2 sides?
Let's call Angle A = 25°, Angle B = 75° and side c = 5.
Angle C is easily found by: ∠C = 180° - ∠A - ∠B
= 180° - 25° - 75°
∠C = 80°
Dropping a perpendicular 'hgt' (for 'height') from Angle C to side 'c', splits triangle ABC into 2 right
triangles.
So, angle BCD =180° - 90° - ∠B =15°
and Angle ACD =180° - 90° - ∠A =65°
Using this information and a trigonometry calculator,
we can find the values of the 2 parts of line 'c'. (see diagram below).
Now, the remaining calculations are quite straightforward.
side a = .55535 ÷ sine(15°) side a = .55535 ÷ .25882
side a = 2.1457
side b = 4.4447 ÷ sine(65°) side b = 4.4447 ÷ .90631
side b = 4.9042
Two Sides and a Non-Included Angle
When solving for a triangle with 2 known sides and a non-included angle,
there may be no solution, one solution or even two solutions.
In a triangle of sides 'c', 'a' and its opposite Angle 'A', the number of solutions is calculated by:
• If a < c•sin(A) no solution
• If a = c•sin(A) one solution: ∠C=90° ∠B=(90°-∠A) and side b=(c•cos(A))
• If c>a>c•sin(A) two solutions.
• If a>=c one solution
Example
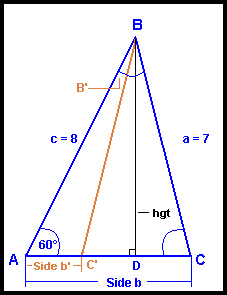
A triangle has sides of 7 and 8 and a non-included angle of 60°
What are the other angles and the other side?
Let's say side a=7, c=8 and Angle A=60°
Dropping a perpendicular 'hgt' from Angle B, we find its length by:
hgt = sine 60° • 8 = .86603 • 8 = 6.9282
 Angle C = arc sine (hgt ÷ side a) = arc sine (6.9282 ÷ 7) = arc sine (.98974)
Angle C = arc sine (hgt ÷ side a) = arc sine (6.9282 ÷ 7) = arc sine (.98974)
Angle C = 81.785°
Angle B is easily found by: ∠B= 180° -60° - 81.785°
Angle B = 38.215°
Side b = AD + DC
To solve these, we'll use the Pythagorean Theorem:
Side AD² = c² - hgt² = 8² - 6.9282² Side AD=4
Side DC² = a² - hgt² = 7² - 6.9282² Side DC=1
Side b = AD + DC = 4 +1 Side b = 5
Is there a second solution?
If c>a>c•sin(A) there are 2 solutions.
8 > 7 > (8 • sin (60°))
Since 8 > 7 > 6.92824, there are two solutions.
Whenever there are two solutions, ∠C and ∠B will each
have 2 values.
We will designate the "second Angle C" as C' and we find it by:
∠C' = 180° - ∠C ∠C' = 180° - 81.789°
∠C' = 98.213°
We find ∠B' by:
∠B' = 180° -∠A - ∠C'
∠B' = 180° -60° - 98.213°
∠B' = 21.787°
Since side b = AD + DC, then side b' = AD - DC = 4 - 1
Side b' = 3
For a calculator and a further explanation of side-side-angle triangles, please click here.
Two Sides and the Included Angle
Example
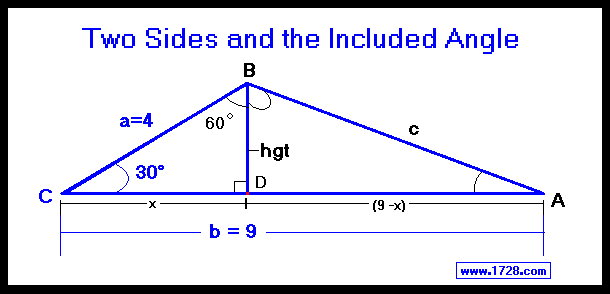
A triangle has sides of 4 and 9 with an included angle of 30°. What are the other 2 angles and the
length of the other side?
Let's say side a=4 and side b=9 and angle C=30°
Dropping a perpendicular 'hgt' from Angle B to side 'b', splits triangle ABC into 2 right
triangles and splits side b into 'x' and '9-x'.
So, angle CBD =180° - 90° - ∠C = 60°
hgt= sine 30° • 4 = .5 • 4 hgt = 2
Line segment 'x' = sine 60° • 4 'x' = .86603 • 4 'x' = 3.4641
Line DA (or 9-x) = 9 - 3.4641 = 5.5359
 Arc tangent (A) = 2 ÷ 5.5359 = .36128 Arctan(A) = .36128
Arc tangent (A) = 2 ÷ 5.5359 = .36128 Arctan(A) = .36128
∠A = 19.864°
Arc tangent (DBA) = 5.5359 ÷ 2 = 2.7680 Angle (DBA) = 70.136°
Angle B is found by adding CBD and ABD which equals 60° + 70.136°
∠B = 130.136°
(We could have found Angle B just as easily by ∠B = 180° - ∠A - ∠C)
Side c = 2 ÷ Sine 19.864° = 2 ÷ .33979 = 5.886
Side c = 5.886
(We also could have found side 'c' by using the Pythagorean Theorem).
All Three Sides Of A Triangle
EXAMPLE:
A triangle has sides of length four, five and six. What are all 3 angles?
Let's say that side a=4, side b=5 and side c=6.
Yes, this could be solved in many different ways, but here's a "neat" solution.
Remember Heron's formula from the triangle page? It states that
triangle area = Square Root (s•(s-a)•(s-b)•(s-c))
where 's' is the semi-perimeter of the triangle.
s=(4 + 5 + 6) / 2 s= 7.5
area = Square Root (7.5 •(7.5 -4)•(7.5 -5)•(7.5 -6))
area = Square Root (98.4375)
area = 9.9216
So, how does this help solve the triangle? Well, there is another area formula:
triangle area = ½ • base • height and therefore,
height = (2 • area ÷ base)
height = (2 • 9.9216 ÷ 6)
height = 3.3072
∠B = arc sine (hgt ÷ side a)
∠B = arc sine (3.3072 ÷ 4)
∠B = arc sine (.8268)
∠B = 55.771°
∠A = arc sine (hgt ÷ side b)
∠A = arc sine (3.3072 ÷ 5)
∠A = arc sine (.66144)
∠A = 41.41°
We then easily solve Angle C using this equation:
Angle C = 180° -55.771° - 41.41°
∠C = 82.819°
Go To Page One
Basic Trigonometric Functions
Go To Page Two
Solving Oblique Triangles Using Law of Sines and Law of Cosines
Return To Home Page
Copyright © 2000 1728 Software Systems
|