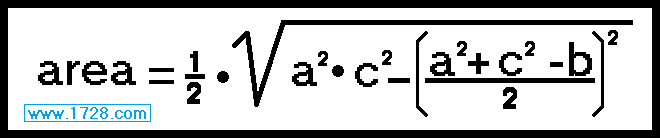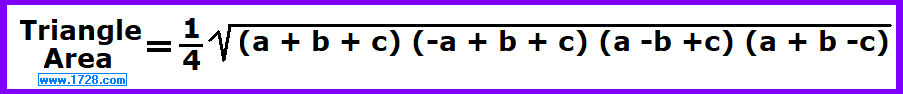Types of Triangles
Scroll to the bottom for the triangle area calculator
|
| |
|
All triangles have 3 sides and 3 angles which always add up to 180°.
The Triangle Inequality Theorem states that:
The longest side of any triangle must be
less than the sum of the other 2 sides.
Triangles are classified in 2 ways-
1) By the number of equal
sides they have:
• scalene - all 3 sides have different lengths
• isosceles - 2 sides have equal lengths
• equilateral - all 3 sides are equal
2) By the types of
angles they have:
• acute triangle - all 3 angles are acute (less than 90°)
• right triangle - has one right angle (a right angle = 90°)
• obtuse triangle - has one obtuse angle (an obtuse angle is greater than 90° and less than 180°).
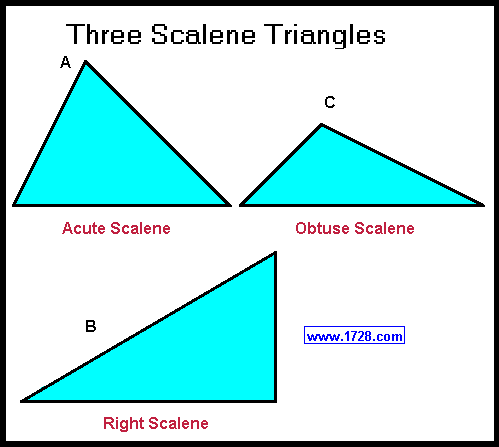
When these 2 categories are combined, there are 7 possible triangles:
• acute scalene (diagram A)
• right scalene (B) - all right triangles are scalene (except diagram E).
• obtuse scalene (C)
• acute isosceles (diagram D)
• right isosceles (E) also known as a 45° 45° 90° triangle.
• obtuse isosceles (F)
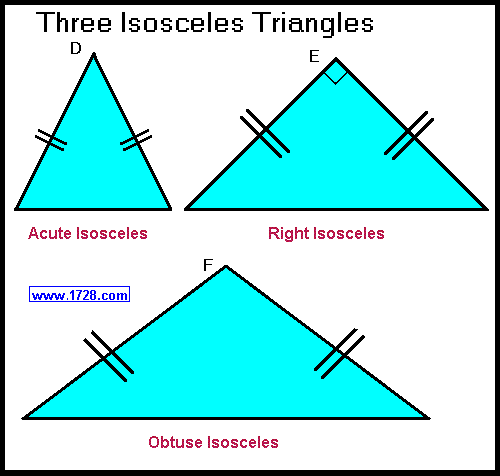
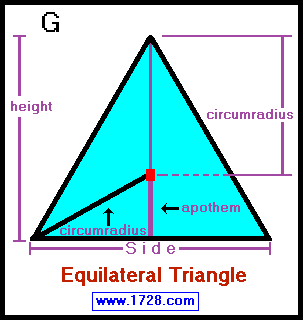
• equilateral (G) all sides are equal and each angle = 60°, making this the
only equiangular triangle.
Since all 3 angles are less than 90° all equilateral
triangles are acute triangles.

There is one more type of triangle that is worth mentioning.
An oblique triangle is any triangle that is not a right triangle.
3 Triangle Area Formulas
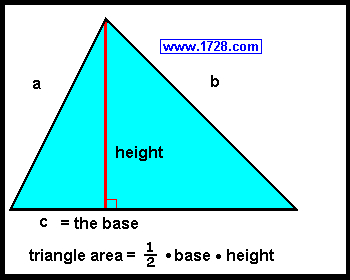
1) The most well-known triangle area formula is multiplying the length of the base by the
height (also called the altitude), and dividing that by 2.
2) If you know the length of all 3 sides of a triangle, you can calculate the area by using
Heron's Formula (sometimes called Hero's Formula).
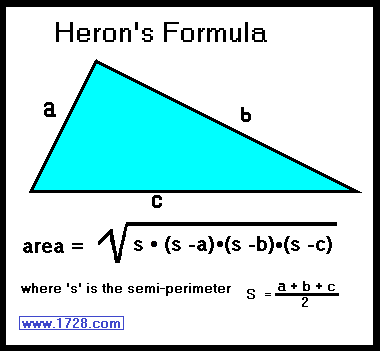 First we have to define a triangle's perimeter which is (side a + side b + side c).
First we have to define a triangle's perimeter which is (side a + side b + side c).
A triangle's semi-perimeter (or 's') is one half of the perimeter or to put it another way:
semi-perimeter = (side a + side b + side c) ÷ 2
Example: A triangle has side a = 4, side b = 5 and side c = 6. What is its area?
The perimeter = 4 + 5 + 6 = 15.
The semi-perimeter is one half of this or 7.5
Using Heron's formula,
area = square root (s • (s - a) • (s - b) • (s - c))
area = square root (s • (s - 4) • (s - 5) • (s - 6))
area = square root (7.5 • (7.5 - 4) • (7.5 - 5) • (7.5 - 6))
area = square root (7.5 • (3.5) • (2.5) • (1.5))
area = square root (98.4375)
area = 9.921567416...
* * * * * * * * * * * * * * * * * * * * * * * * * * * * *
By algebraic manipulation we can state Heron's Formula in two more ways.
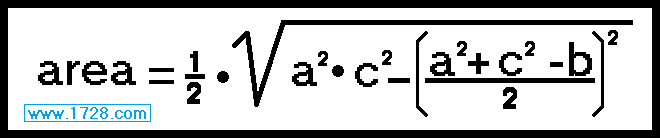
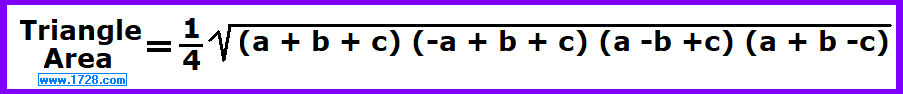
* * * * * * * * * * * * * * * * * * * * * * * * * * * * *
|
|
3) If you know 2 sides and an included angle, there is a third formula for determining triangle area.
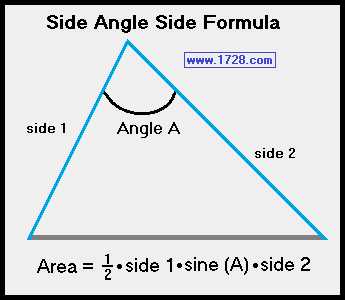 This formula applies to all triangles and not just right triangles.
This formula applies to all triangles and not just right triangles.
Area = ½ • side 1 • sine (A) • side 2
This is an easy formula to prove. First, we use the traditional formula:
Area = ½ • height • base then we can substitute side 2 for the base:
Area = ½ • height • side 2
Since sine (A) = height / side 1 then height = side 1 • sine(A)
and then area = ½ • side 1 • sine (A) • side 2
Triangle Area Calculator
This calculator determines triangle area by using any of the 3 methods above.
If you need a more advanced triangle calculator then click here.
Return To Home Page
Copyright © 2000 1728 Software Systems
|