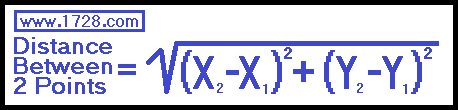|
|
Slope, Distance and Equation Calculator
A calculator for determining the slope of a road is located here.
|
|
|
When 2 Points Are Known
I N S T R U C T I O N S
Creating Equation When 2 Points Are Known
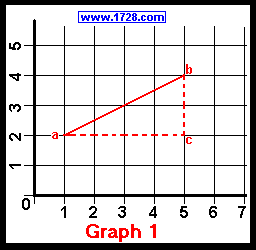 As an example, we'll start by choosing 2 points: a (X1, Y1) and b (X2, Y2)
As an example, we'll start by choosing 2 points: a (X1, Y1) and b (X2, Y2)
Their actual values are: a (1, 2) and b (5, 4).
Calculating the Slope
In mathematics, slope (designated by the letter 'm') is defined as the ratio of the 'Y'
axis to the 'X' axis between 2 points.
In less formal terms this is called the "rise over the run".
The equation for determining the slope between 2 points is:
Slope or m = (Y2 -Y1) ÷ (X2 -X1)
As stated above, point 'a' has the values of x1 = 1 and y1 = 2
and point 'b' has the values of x2 = 5 and y2 = 4.
Using the slope formula, we can determine the equation's slope from these 2 points.
m = (4 - 2) ÷ (5 - 1)
m = 2 / 4
m = ½ or .5
Calculating the Equation
(y - y1) = m • (x -x1)
Utilizing the above expression, we can now calculate the equation.
We've already calculated the slope which is .5, so now we'll need just one point. Let's choose (1, 2)
Filling in the above equation with the slope and this point we get:
(y - 2) = .5 • (x -1)
y = .5 • (x -1) + 2
y = .5x -.5 + 2
So, the equation shown in the above graph is: y = .5x + 1.5
If we needed to calculate the slope angle we merely take the arc tangent of the slope.
In this case, arc tangent(.5) = 26.565...degrees.
Calculating the Distance
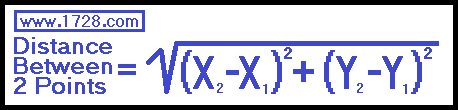
To find the distance between the two points, we utilize the above formula which is based upon the Pythagorean Theorem,:
Distance = Square Root ((4 - 2)2 + (5 - 1)2)
Distance = Square Root ( 22 + 42 )
Distance = Square Root ( 20 )
Distance = 4.4721 ...
Calculating the Equations:
When 1 Point and X-intercept Are Known
We can calculate the second point from the x-intercept, because the y value for the x-intercept will always be 0.
So, if the x-intercept is -3 then that second point is (-3, 0).
When 1 Point and Y-intercept Are Known
We can calculate the second point from the y-intercept, because the x value for the y-intercept will always be 0.
So, if the y-intercept is 1.5 then that second point is (0, 1.5).
Calculating the Equation
When Slope and 1 Point Are Known
|
Example:
A line has a slope of 9 and passes through the point (7,5).
What is the equation?
We calculate "b" from this equation:
b = y - mx
b = 5 - (9 • 7)
b = -58
Next, we enter the value of "b" and the slope into this equation:
y = mx +b
y = 9x -58
Use this example in the calculator below.
|
| |
Return To Home Page
Copyright © 1999 -
1728 Software Systems
|